今回は化学結合について考えていきます。高校化学で学習した多くの結合の中から、その中でも共有結合についてみていきましょう。

高校の化学では共有結合の他にも金属結合、イオン結合、分子間力などについても学習した覚えがあります。

その中でも共有結合についてより深く学習していきましょう。特に、二重結合・三重結合が重要になりますね。
共有結合とシグマ結合

電子軌道を使って共有結合を考える前に、高校レベルの知識について復習しておきましょう。高校化学では2個以上の原子が電子を共有して結合を作り、分子を形成するのでした。また、その共有された電子を共有電子対といいましたよね。

このくらいはしっかり覚えていますよ。確か共有電子対は単結合なら1つ、二重結合なら2つ、三重結合なら3つあるんでしたよね。電子の個数はその2倍ですよね。

その通りです。二重結合や三重結合といった多重結合についてもばっちりですね!今回はその共有電子対についても話が出てきます。この後の話で、軌道と共有電子対を関連付けて理解しましょう。
電子軌道と波動関数
まずは電子軌道と電子密度の関係性について復習していきましょう。電子軌道とは\(s\)軌道や\(p\)軌道のことで、電子の存在確率、つまり電子密度が大きな領域を図示しているものでした。以下の記事も合わせて読んでみましょう。
高校化学では原子はお互いが電子を出し合い、共有電子対を介して結合を作ると理解します。しかし実際は、電子は粒子として原子核の周りをまわっているわけではなく、波動関数に従った運動をしているだけでした。
大学の化学で学習する電子の運動を表す波動関数と、高校化学で学習する共有電子対をつなげて考えるためにはどうすれば良いでしょうか?

うーん…。電子が粒子なら2つの原子が共有するのもなんとなく理解できるんですけど…、波動関数とか絡んでくるとよくわかりません。

波動関数がそもそも何を表しているのかを考えるところから始めましょうか。
【復習】波動関数は電子の存在確率
波動関数は電子の運動を表している関数ですが、この関数単体だけでは何もわからず工夫をする必要がありましたよね。その中でも、波動関数の2乗が電子の存在確率を表すということがあったのを覚えていますか?
そして、その存在確率がある一定の大きさを持つエリアを図示したものが電子軌道の正体でした。そのため、この電子軌道中に電子が存在するとみなしてOKです。
【復習】波の重ね合わせと位相
少し話がそれますが、ここで高校物理で学習した波についても復習しておきましょう。波の性質には「位相」がありました。この位相に関して、今回の波動関数の理解のためには、波動関数が正負の符号を持つことを覚えてくれれば良いでしょう。

位相が同じ波を重ねるとその波は強め合い、逆の位相であれば弱め合うということも思い出しておきましょう。
軌道の重ね合わせ
さて、「共有電子対と波動関数・電子軌道」の関係性について解説していきます。1つ1つの原子には\(s\)軌道や\(p\)軌道といった各々の電子軌道が存在します。原子同士が近づくとこの電子軌道同士も近づき、波動関数が重なります。

ここで電子軌道の重ね合わせが生じるのですか?

その通りです。波動関数または電子軌道が重なると強め合い・弱め合いが起こります。まずは\(s\)軌道だけを持った原子2つが近づく場合を考えてみましょうか。
\(s\)軌道の符号と重ね合わせ
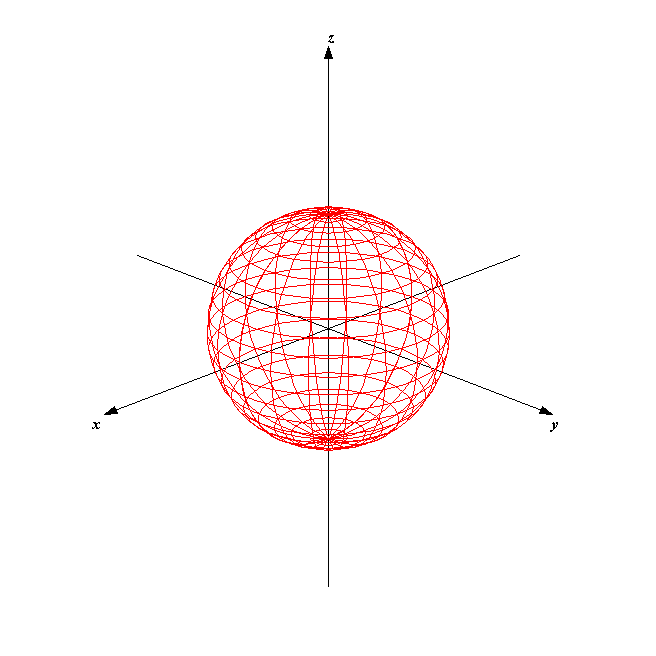
まずは\(s\)軌道について思い出してみましょう。\(s\)軌道は下の図のような形をしていて、さらに符号は全体がプラスでしたね。
Azu – Function View ver560c にて作成, CC 表示 3.0, リンクによる
wikipedia s軌道より引用
この軌道を持った原子2つが近づいた時を考えてみます。2つの電子軌道が近づくともちろん、重ね合わせが生じます。\(s\)軌道はもちろん全体の符号が同一なので、重ね合わせが起きるとお互いに強め合います。
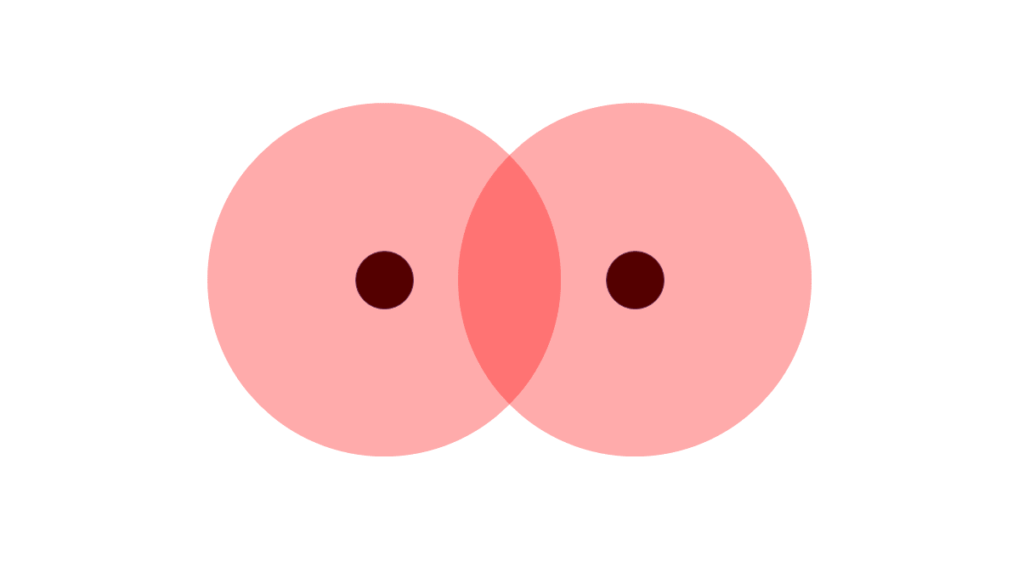
普通の波が強め合うと振幅が大きくなりますが、波動関数の場合は電子密度、つまり電子の存在確率が大きくなります。重ね合っている部分はもちろん原子同士の間の空間なので、原子間に電子が存在する確率が他の場所よりも大きくなっているといえます。

なるほど。高校化学で学習した原子間にある共有電子対は、波動関数の強め合いから生じる電子の存在確率UPと関連しているんですね!
\(p\)軌道の符号と重ね合わせ
Azu– Function View ver560c にて作成、Adobe Photoshopにて加工
CC 表示 3.0 ,リンクによるwikipedia p軌道より引用
それでは\(p\)軌道はどうでしょうか?\(s\)軌道と異なり、\(p\)軌道ではプラスの符号だけでなくマイナスの符号を持った軌道もあります。

もしかして符号が同じだと強め合うように、符号が違う軌道が重なると、弱め合ったりするんですか?

そのあたりは高校物理で学習した波と同じですよね。強め合えば電子の存在確率がアップするように、弱め合えばその確率がダウンします。
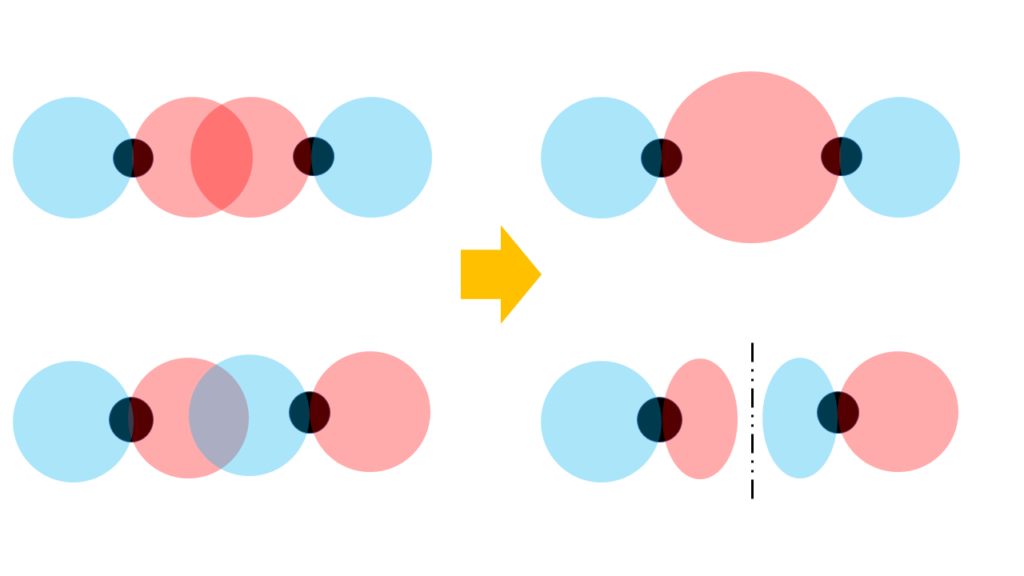
今回重要なのは同符号の軌道が重なると電子の存在確率が大きくなることですので、弱め合う場合はまたの機会に回します。ちなみに、この強め合う・弱め合うという考えは「分子軌道」の考え方で重要となります。
シグマ結合とは?
これまでに見てきたような電子軌道と電子軌道が重なった結果、電子の存在確率が上がって作られる結合の事を「シグマ結合」といいます。共有結合はほぼすべてこの結合であり、これは\(s\)軌道と\(p\)軌道が重なった場合も同じです。

\(s\)軌道同士、\(p\)軌道同士の重なりも\(s\)軌道と\(p\)軌道の重なりも同じように強め合ったり弱め合ったりするんですね。
多重結合とパイ結合

二重結合や三重結合の場合はどうでしょうか?多重結合の場合は単結合、つまりシグマ結合とは少し異なります。それではどこがシグマ結合と違うのか見ていきましょう。
\(p\)軌道の重なり
先ほど見てきた\(p\)軌道同士はお互いの方向を向いており、軌道同士がしっかりと重なっている様子が見られ、この時に形成される結合をシグマ結合というのでした。それではこの軌道が異なる方向、例えば下の図のような方向に向いていたとしたら結合は形成されるでしょうか?
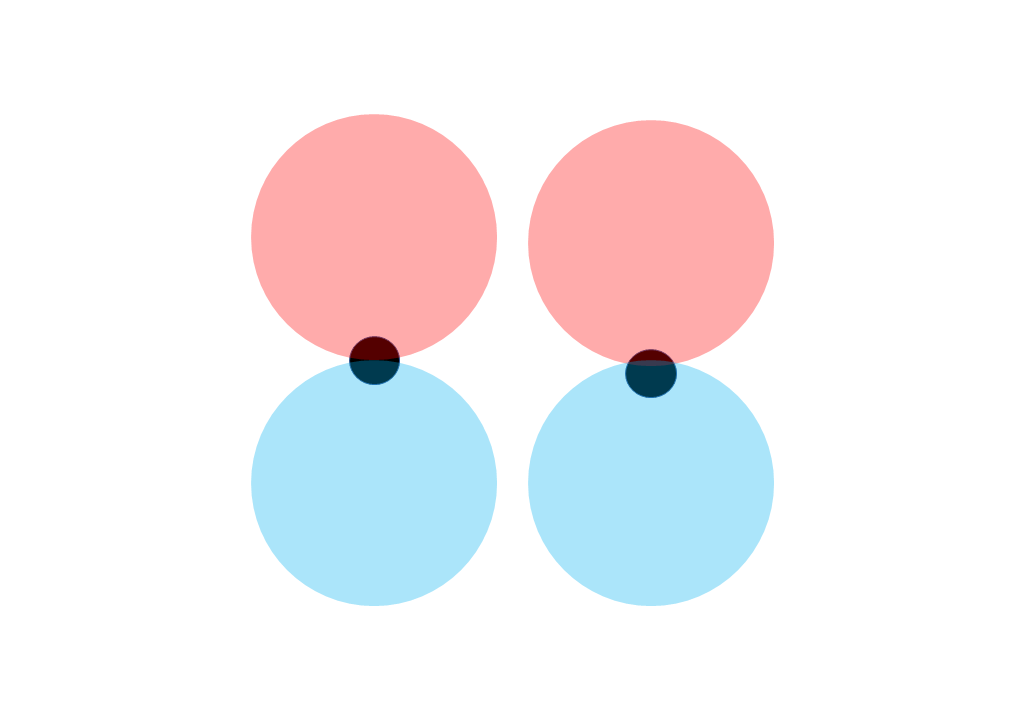

んー。なんか軌道同士は重なっていないように見えるので、結合はできないような気がします。
結合は形成される
実は\(p\)軌道は重なっていなくても結合が生成されます。このように軌道が直接重なっていなくても形成されるような結合をパイ結合といいます。
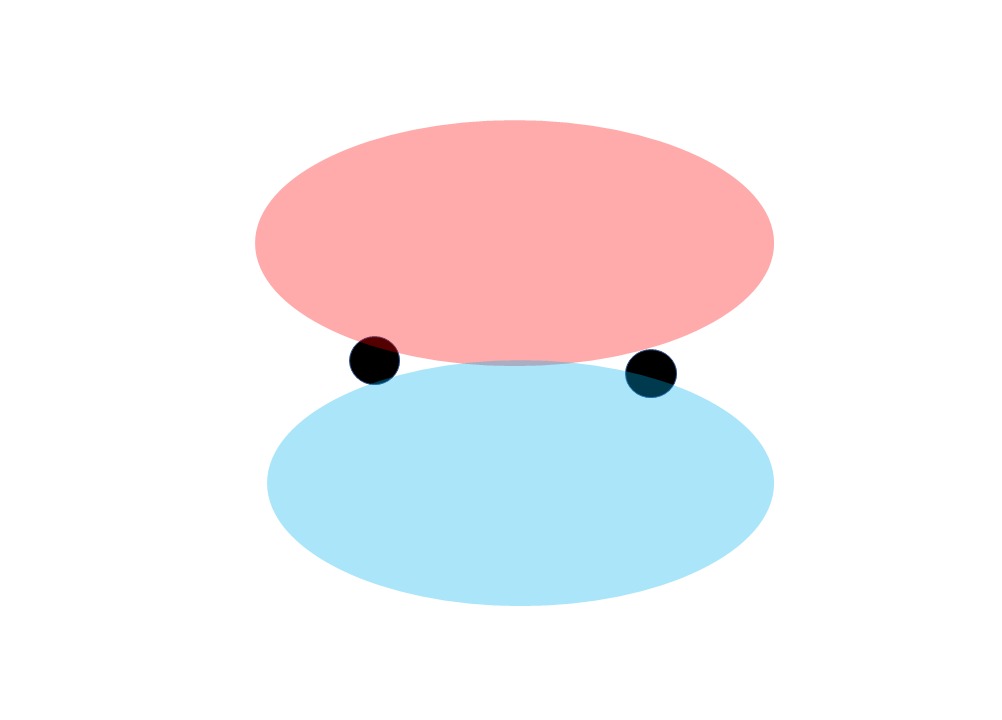

このパイ結合は高校化学での結合の考え方とは少し違っています。下に図も載せますので、何がシグマ結合と違うのかしっかり押さえましょう。
二重結合と三重結合
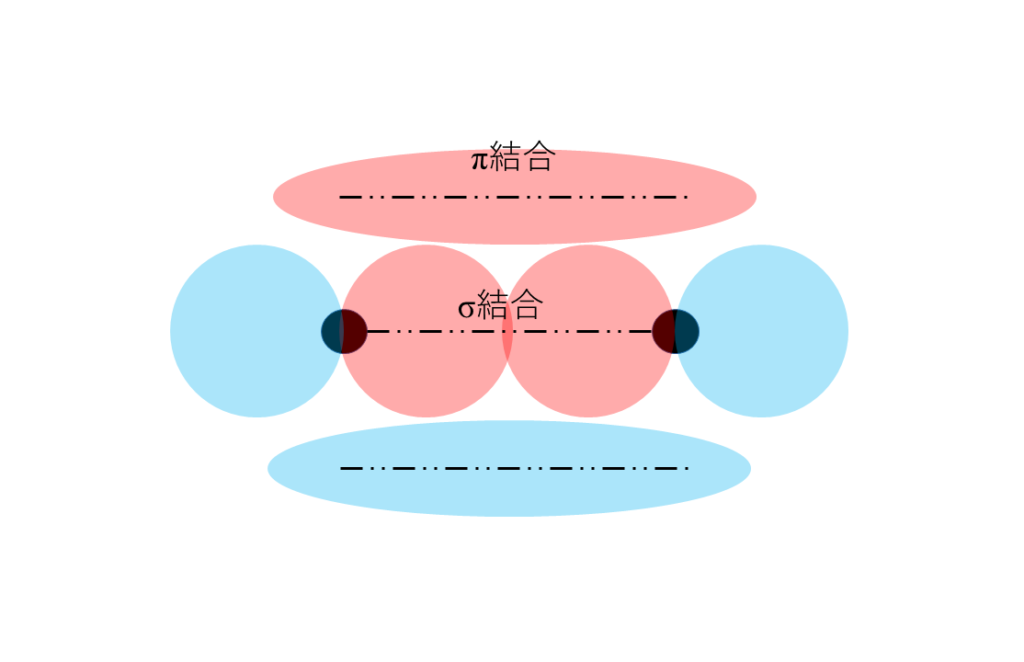
このパイ結合というのは、二重結合や三重結合といった結合を考える際に重要になってきます。二重結合とは、全く同じ結合が2つ作られるわけではなく、シグマ結合が1つとパイ結合が1つで二重結合が作られます。
同じように三重結合はシグマ結合が1つとパイ結合が2つで三重結合を形成します。三重結合を考えるときは\(xyz\)空間座標におけるそれぞれの軸方向で考えないといけません。普通は\(z\)軸方向にシグマ結合を1つ、\(x\)軸方向と\(y\)軸方向にパイ結合を2つ作ると考えます。

なるほど!2本や3本の線でいつも書いていた結合にシグマ結合とパイ結合が含まれていたんですね!

その通りです。そしてその2つの結合は電子軌道の重なり方が違います。この重なり方の違いがエネルギーにも響いてきますが、それは分子軌道を考えるときにお話ししましょう。
多重結合の軌道
最後に二重結合での軌道の重なり方を図を使ってみていきます。ここでは2つの\(p\)軌道を用いて結合を説明しますが、実際の結合はそこへ\(s\)軌道の寄与も含めた混成軌道を使って考えなければいけません。

その点は注意しましょう。テストなどでそのまま使うとバツになってしまいますよ。
ちゃんと混成軌道を使った二重結合・三重結合については次の機会にお話ししますので、混成軌道はしっかり理解しておきましょうね。
今回の要点
今回はシグマ結合とパイ結合の違いを\(s\)軌道や\(p\)軌道を使ってみてきました。実際には上で言ったように、混成軌道を使って考えなければいけないのですが、両者の違いを理解するだけならこれで十分です。

結局2つの違いは、電子軌道がお互いの方向に向き合って結合を作っているか、そうでないかの違いでしたね。

よく理解できているようですね。この考え方がきちんとできていれば、混成軌道中で2つの結合を考えても大丈夫でしょう。







コメント