それでは、前回出てきた「シュレディンガー方程式」を解いてみましょう。シュレディンガー方程式や電子の粒子性・波動性について、量子力学・量子化学についての考え方に関しては以下の記事を参考にしてみてください。

今回はシュレディンガー方程式の中では、最も簡単なパターンである「1次元箱型ポテンシャル」についての問題を数学的に解いてみます。
シュレディンガー方程式を立式

1次元箱型ポテンシャル中の電子についてのシュレディンガー方程式を立式してみましょう。シュレディンガー方程式の立式ではまずハミルトニアンを考えることが必要です。
そして、そのハミルトニアンを考えるためには、そもそも今回扱う「1次元箱型ポテンシャル」という状況をしっかり考えてみる必要があります。わかりやすく解説しますし、いったん分かってしまえば難しいことは言っていないので少しずつ進めていきましょう!
1次元箱型ポテンシャルとは?
いきなり普通のたくさんの電子が含まれる原子や分子を考えることは難しいため、まずは最も簡単な状況を設定したうえでシュレディンガー方程式を立式します。
そして今回考える1次元箱型ポテンシャルとは以下の図のような状況にある電子を示します。
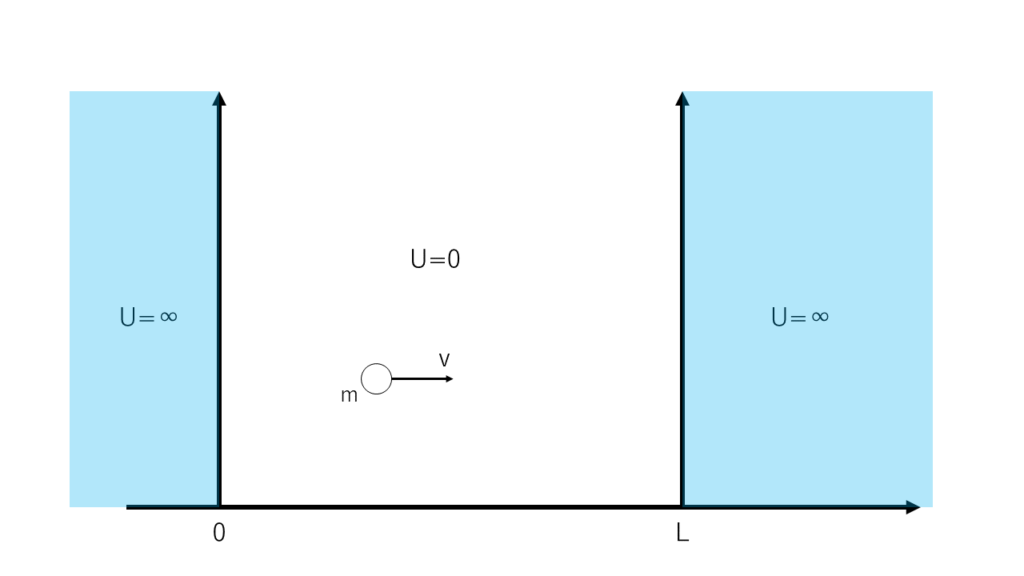
簡単に状況を解説しましょう。上図中の横軸は\(x\)軸を示しており、\(0\leq x\leq L\)を満たす白で塗られた範囲では位置エネルギー(\(U\))が\(0\)となり、それ以外の青で塗られた範囲は位置エネルギー(\(U\))が\(\infty\)となるような状況を考えます。また電子の質量は\(m\)、速度は\(v\)を持つとします。
ここで、なぜ位置エネルギーを\(\infty\)とするのかという疑問を解決しておきましょう。もし電子が白く塗られた領域から青く塗られた領域に入るとします。このとき電子は\(\infty\)を超えるエネルギーを持っていなければ領域を移動することができません。しかし電子の持つエネルギーに無限大はありえないので、青い領域に電子は入ることができません。

高校物理の位置エネルギーで言い換えてみましょうか。坂道を駆け上がるにはエネルギーが必要なので、無限大に高い坂道の頂上に行くためには無限大以上のエネルギーが必要です。しかし「無限大のエネルギー」なんてものは存在しないので電子は青い領域に入る(坂道を駆け上がる)ことはできません。
つまり、1次元箱型ポテンシャルのような状況を設定すれば、粒子の運動を考える範囲は位置エネルギーが\(0\)である白の領域だけでいいわけです。青の領域には入れませんからね。この話はトンネル効果などにつながってきますが、ここでは省略します。

トンネル効果については下の記事でわかりやすく解説しています。「トンネル効果」とは、位置エネルギーが有限のときに起きる不思議な現象です。
ハミルトニアンを考える

1次元箱型ポテンシャルの状況が理解できたところで、いよいよシュレディンガー方程式の立式に取り組んでいきます。先ほど言った通り、シュレディンガー方程式の立式に必要なものは「ハミルトニアン」です。1次元箱型ポテンシャルの場合のハミルトニアンは、電子の運動エネルギーと位置エネルギーの和から求めることができます。

ポテンシャルは位置エネルギーと覚えておくととても便利です。教科書ではポテンシャルとしか出てきませんので注意しましょう。
今回かんげるべきなのは白い領域だけなので、そこでの運動エネルギーと位置エネルギーを考えてみましょう。高校物理の基礎中の基礎なのでここの導出はさすがに大丈夫だと思います。運動エネルギーと位置エネルギーはそれぞれ次のようになりますね。
$$E=\frac{1}{2}mv^2$$
$$U=0$$
この2つのエネルギーの和をとってみると\(E+U=\frac{1}{2}mv^2+0\)となります。さてここからが少し奇妙な操作を行いますので、わかりやすく説明をしていきます。
まずは先ほど求めておいた運動エネルギーと位置エネルギーの和を運動量を用いて書き換えます。これはこの後の置き換えをするために行います。この変形を適用すると\(p=mv\)から\(v=\frac{p}{m}\)となるので\(\frac{1}{2}mv^2=\frac{1}{2m}p^2\)と書き換えることができます。

ここから「少し不思議なこと」をするのですがこれは古典力学と量子力学を結びつけるために行うものです。式変形やその他諸々は長くなるので、後ろの方で付録として少し詳しく説明しましょうか。
さて、その不思議なことというのは運動量\(p\)を置き換えます。
$$p→-i\hbar\frac{\partial}{\partial x}$$
「なぜか?」と問いたくなるのも分かります。これまでこんなことやりませんでしたからね。私も初めて出会ったときにはその疑問を持ちましたが、その疑問はひとまず置いておきましょう。解いていくうちにわかってくることもあるものですよ。そしてこのような変形を行うとシュレディンガー方程式に使えるハミルトニアンが完成します。
シュレディンガー方程式

シュレディンガー方程式は\(H\psi=E\psi\)でしたね。上でエネルギーの和から導出したシュレディンガー方程式のハミルトニアンを使うと、方程式の全体像は下のようになります。
$$-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\psi=E\psi$$
シュレディンガー方程式の全体像と演算子
前回少し出てきましたが、このような\(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\)のようなものを「演算子」といいます。微分や積分の範囲でよくみる記号です。ちなみに今回出てきた記号は偏微分と呼ばれる微分のことで、注目している変数以外はすべて定数として扱う微分のことです。

つまり、何かを足したり引いたりするのではなくこの関数について”微分します”や”積分します”といった「操作」を伝えるために使われるのが「演算子」というものです。
シュレディンガー方程式を解く
今回はシュレディンガー方程式を立てるまでで止めておいて、次回に立式したシュレディンガー方程式を実際に解いてみます。
この1次元箱型ポテンシャルはシュレディンガー方程式が解ける数少ないパターンのうちの1つです。2個以上の電子が含まれる原子や分子では電子間の反発がハミルトニアンに入ってきてしまい、これが原因で解を出すうえで必須となる「変数分離」という操作ができなくなるために解けなくなるのです。なので数学的に解く方法はこの問題だけ押さえておきましょう。
ちなみに2個以上の電子が含まれるパターンは厳密には解けませんが、近似等を用いることで解を出すことはできます。この話もいずれしましょうか。
今日の要点
- シュレディンガー方程式には古典的なエネルギーが必要
- 運動量を演算子で置き換えることで完成する
- 数学的に解けるのは1次元箱型ポテンシャルだけ。
付録
さて、なぜ置き換えでうまくいくのか?ということですが、これを説明するにはド・ブロイ波の説明からしなければなりません。

ド・ブロイ波とは物質波とも呼ばれ、物質が持つ波のことだという認識でOKです。二重性の話ですべての物質は粒子性と波動性を持っていると出てきましたよね?
粒子の粒子性を特徴づけるものとして「位置」や「運動量」があり、波動性を特徴づけるものとして「波長」や「周波数」があります。しかし、物質が波の性質を持つことが実験によって確かめられたので、粒子性と波動性を結びつけるものが必要となりました。
そこでこれらを数式で表し、ド・ブロイ波として組み合わせて計算を行うとハミルトニアンを作る際の「置き換え」が導出できます。しかしここでは量子力学ではなく量子化学に焦点を当てるため、詳細な計算過程は割愛していきます。おすすめのサイトリンクを貼っておきますね。
さらに量子論では古典的な力学とは異なり、固有方程式と呼ばれる方程式から導かれる固有値によって各物理量が決まります。つまり実験において古典的な物理量Aを観測した結果というのはこの固有方程式を解くと得られた「固有値」であるということです。
この固有方程式を解くことで得られる「固有値」は方程式によっては1つとは限らないため、いくつもの観測結果が得られることもあります。どの結果が得られるかは確率的であり、特殊な場合を除いて1つには決まっていません。

このようなところに「量子論」の面白さが見えます。いくつもの状態が重なっていると見なせるため「重ね合わせ」といわれることもあり、この考え方の応用が量子コンピュータなどで使われています。
この固有方程式に使われるのが先ほど出てきた「演算子」であり、シュレディンガー方程式も(エネルギーの)固有方程式です。
これ以上の細かいことはもっと勉強が進んでから次第に理解できるようになることもあるので、今はまずこの奇妙な「置き換え」という操作を認めてしまいましょう。笑
参考文献
量子化学ー基礎からのアプローチ(真船 文隆)
詳解 量子化学の基礎(類家 正稔)
はじめての量子化学 量子力学が解き明かす化学の仕組み(平山 令明)









コメント