今回はみなさん苦手な\(s\)軌道、\(p\)軌道…などの軌道について詳しく見ていきます。教養課程で化学を取ってしまったけれども、電子軌道についてわからず詰みかけている人に対してわかりやすく解説していきます。

僕も高校の時に化学が得意だったので、講義を取ってみたのですが、何が言いたいのかがあまりわかっていません。このままではテストと単位がやばそうです。

大学では高校と違って先生にも聞きづらいですからね。ここで基本的なことは解決しておきましょう。実は意外と難しいことは言っていません。
電子軌道とは?

そもそも電子軌道とはなんでしょうか?これを理解するためには電子が持つ「波動性」と「粒子性」の2つについて知っておく必要があります。ただし、深い理解などは必要ありません。
電子はこの2つの性質を持っているがゆえに、高校物理で学習したような力学や電磁気に出てくるような単純な方程式では表せないということだけわかっていればOKです。

これは上の記事がわかりやすく解説していましたね。電子は粒子としての性質と干渉などの波としての性質を持っていたのを覚えています。
電子の存在確率
このようないわゆる「二重性」を持った物質の運動を表すために考え出されたのが「シュレディンガー方程式」でした。そして、このシュレディンガー方程式から波動関数とエネルギーが求められ、この波動関数の2乗が電子の存在確率を示すのでしたよね。
つまり電子は高校で習ったように、どこか決まった道のような軌道を回っているのではなく、原子核周辺のどの位置にでも現れる可能性があるということです。
しかしその観測される位置には、電子が現れやすいところとそうでないところがあり、よく観測されやすい場所のことを軌道と考えましょう。
軌道の考え方
このよく観測されやすいところをピックアップしたのが電子軌道です。繰り返しになりますが、これは高校で学習した\(K\)殻や\(L\)殻のような決まった道のようなものではなく、波動関数から求めた確率を基に考えられたものです。

波動関数の2乗が確率を表すことは覚えていますか?電子などのミクロな粒子の運動は波動関数を考えなければいけなかったはずです。
例えば、電子が観測される確率80%以上のところに印をつけていったとしましょう。そうすればある程度、その印が原子核を中心とした殻のような形状に集まった図となります。これが「電子軌道」であり、あくまで波動関数から考えた確率であることを頭に入れておいてください。
そしてこの印を集めてきれいに描いたものがよく目にする軌道です。教科書などに出てくる\(s\)軌道や\(p\)軌道と紹介されている図ですね。つまり、あの図はある一定の確率以上で電子が観測される場所を表しているものにすぎません。

2次関数のように、式を満たす点を座標平面に打って行くと、グラフになるみたいな話と同じってことですよね。球状に広がっているからちょっとわかりづらかったです。
軌道の種類とその形状

軌道についてよく理解できたところで、いろいろな軌道を見ていきます。軌道には\(s\)軌道、\(p\)軌道、\(d\)軌道…など複数種類ありますが、ここでは3種類だけ見ていきます。

え!なぜ複数あるんですか?

それは量子数がたくさんあるからです。量子数は\(n=1,2,3…\)と続きますが、それに対応して軌道もたくさんあります。ただ、普通はこれから取り上げる3つの軌道を考えることが多いので全部を考える必要はないでしょう。
\(s\)軌道
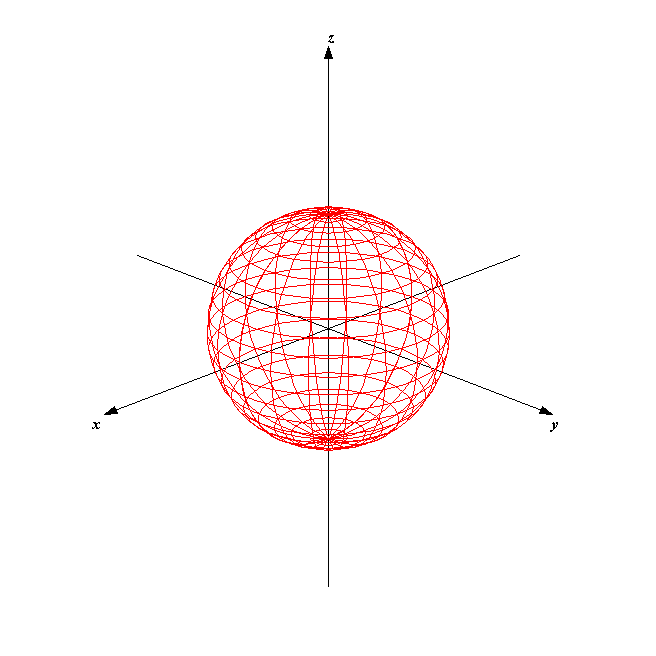
まずは\(s\)軌道から見ていきましょうか。\(s\)軌道は次のような形状をしています。ちなみにこの形状は\(1s\)軌道でも\(2s\)軌道でも大まかには変わりません。
Azu – Function View ver560c にて作成, CC 表示 3.0, リンクによる
wikipedia s軌道より引用
\(s\)軌道の形状
\(s\)軌道は原点を中心として球状に広がっています。これはなんとなく高校で想像していたような軌道のイメージに近いのではないでしょうか?
この電子軌道で1番電子の存在確率が高いのは、中心から少し離れた「殻」の部分になります。つまり、原子核から遠すぎても近すぎても電子は観測し辛いのです。

あー、なんとなくは分かります。しかしなぜそんなことが起こるのですか?

これから少し数学が入った難しい話になるので、なんとなくイメージできれば良いくらいに考えてください。面倒くさい人は次の\(p\)軌道まで飛ばしてもらっても構いませんよ。
距離依存性と角度依存性
波動関数は空間上に広がっており、これを極座標に変換してあげると原点からの距離に依存する部分と角度に依存する部分が出てきます。電子の位置は原子核からの距離と角度で決まるということです。そして、それを決定する変数は3つあり、1つは原子核からの距離\(r\)、残り2つは角度を示す部分です。詳細は以下をチェックしましょう!
よく\(s\)軌道や\(p\)軌道といって出てくる上のような電子軌道図はこの距離依存性と角度依存性のうち、角度依存性だけを表しています。

何を言っているかわからないよ。さっきの「存在確率が高いのは中心から少し離れた殻の部分」ということとどこがつながるの?

実は距離依存性まで考えると、原点からある距離離れた球面上が最も存在確率が高いということになります。つまり横軸に半径、縦軸に存在確率を取ると上に凸の山なりになるということです。
原子核に近すぎても遠すぎても電子の存在確率は0に近づくということです。ちなみに\(1s\)軌道の場合の最も存在確率が高い半径はボーア半径\(a_B\)であることが知られています。

この後出てくる\(p\)軌道や\(d\)軌道についても同じことがいえるので、形状だけを考えましょう。
\(1s\)軌道と\(2s\)軌道の違い
この距離依存性と角度依存性がわかると、\(1s\)軌道と\(2s\)軌道の違いが分かるようになります。同じ\(s\)軌道と言っているぐらいなので形状は変わりません。

分かった!距離依存性の方が違うんですね。確か主量子数\(n\)の違いは高校で習った電子殻の違いと同じだったから、\(2s\)軌道の方が存在確率が最大になるような半径が大きいとか?

そうです!\(1s\)軌道に比べて\(2s\)軌道はもっと原点から遠い位置で電子を見出す確率が高くなります。ただ、どちらも形状は球形なのです。
このように電子軌道を考えるためには、距離依存性と角度依存性は分けて考える必要があるのです。まあ少し難しい話なので、軌道の形や考え方だけを知りたい人は飛ばしてもいいでしょう。引っかかったらまた戻ってこればよいだけの話です。それでは次の軌道を見ていきましょう。
\(p\)軌道
\(p\)軌道の角度依存性をあらわした図は次のようになります。ここで気になるのは赤色と青色の2色であらわされていることですよね。\(s\)軌道のときは赤色だけでした。
Azu– Function View ver560c にて作成、Adobe Photoshopにて加工
CC 表示 3.0 ,リンクによるwikipedia p軌道より引用

この軌道図はなぜ赤色と青色の2色で色分けされているんですか?\(s\)軌道のときは1色しかなかったのに…

これは「位相」というものを考える必要があります。高校の時の波動分野で同じものを扱ったと思いますから、それを思い出しましょう。
軌道の位相とは?
高校物理で位相は波同士が「強め合う」のか「弱め合う」のかを判断する際の材料として重要であったと思います。そしてこの電子軌道においても全く同じ考えで大丈夫でしょう。

つまり波動関数が「強め合え」ば、電子の存在確率はより大きくなり、逆に「弱め合え」ば電子の存在確率もより小さくなります。
この強め合いの考えは原子同士が結合を作って分子になるのを考えるときにとても役立ちます。分子軌道という考えに直結しますからね。
science-univ.com/quantum-chem/molecular-orbital/
ただしそれは2つ以上の波が重なった場合の話であって、波が1つしかない場合、つまりその場所の電子の存在確率を考えるだけであれば何も気にしなくてOKです。赤の領域と青の領域では何の違いもありません。
\(p\)軌道の形状
\(p\)軌道は原点ではなく、各軸上のある点を中心とした球状をしていることがわかります。また、\(x\)軸、\(y\)軸、\(z\)軸に対応して3つあることも特徴ですね。
ここでも図はあくまで角度依存性を表しているということだけ注意しておきましょう。\(p\)軌道はまた\(\sigma\)結合や\(\pi\)結合を考えるときにお世話になります。
\(d\)軌道
最後に\(d\)軌道をみましょうか。\(s\)軌道や\(p\)軌道と違って、\(d\)軌道はなかなか複雑怪奇な形をしています。
Azu – Function View ver560c にて作成、Adobe Photoshopにて加工
CC 表示 3.0, リンクによるwikipedia d軌道より引用
このような複雑怪奇な軌道の形なんていちいち覚えてません。なので必要な特徴だけを押さえましょう。

その覚えておかなければいけない特徴ってなんですか?

よくみればわかりますが、\(d\)軌道の内3つは軸と軸の間に軌道が広がっていますね。反対に残り2つは軸に沿って軌道が広がっています。
この軌道の広がり方は6配位の錯体を考えるときに用いることになります。結晶場分裂や配位子場分裂とかですね。逆に言えば\(d\)軌道を考える場面は、錯体と混成軌道くらいです。
今回の要点
今回は\(s\)軌道、\(p\)軌道、\(d\)軌道を見てきました。どれもよく見る図だとは思いますが、これはあくまで角度依存性を表しているだけであることには注意しましょう。

あとは位相についても覚えておきます。分子軌道とかいうものを考えるのに必要になるんですよね?

そうですね。分子軌道では高校物理の波動と同じように「同位相」や「逆位相」を考えることになります。また5つの\(d\)軌道の軸との位置関係もしっかり押さえておきましょう。
参考文献
量子化学ー基礎からのアプローチ(真船 文隆)
詳解 量子化学の基礎(類家 正稔)
はじめての量子化学 量子力学が解き明かす化学の仕組み(平山 令明)










コメント