
前回までで1次元箱型ポテンシャルについての解説が終わりましたね。この「箱型ポテンシャル」の特徴の1つに、無限大のポテンシャルがあったと思います。今回はそのポテンシャルが有限であった場合について考えてみましょう。

有限だと何か変わるんですか?

ポテンシャルが有限の場合と無限の場合では全く違います。今回も数式が少し出てきますがしっかり解説していきます。
トンネル効果とは?

さてまずは「トンネル効果」について解説しましょう。そのあとに、トンネル効果を数式を用いて示してみたいと思います。これまで学習したであろう波動関数や粒子と波の二重性についてももう1度整理しながら進めましょうか。
波動関数と粒子の存在確率
まず大前提として波動関数とは、物質が粒子と波の2つの性質を持つことによって書かれるあらゆる情報を含んだ関数であるということを思い出しましょう。さらにその関数の2乗は粒子が存在する確率を示していました。
そして1次元箱型ポテンシャル中では、「箱の外では粒子が観測できない」という条件の下で計算を行いました。つまりポテンシャルが無限大であるという極限を考えていたわけです。

この極限が何か関係あるんですか?

トンネル効果とはこの極限の条件を緩めた時、つまりポテンシャルが無限大でない場合に起こる現象です。
1次元箱型ポテンシャルでは箱の外では粒子を絶対に観測できない場合を考えたので、波動関数はその値が\(0\)となります。しかし、もし波動関数が箱の外でも\(0\)以外の値を持つとすると、この「絶対に観測できない」ということが変わってきます。つまり、波動関数が箱の外にも伝播するのであれば、そこには粒子の存在確率があるということになるので、粒子を箱の外でも観測できるということになります。

このことは波動関数の意味を再確認すると良いでしょう。波動関数の2乗は粒子の存在確率を示すので、箱の外で\(0\)でない値を持つのならば、粒子の存在確率も\(0\)ではなくなります。
トンネル効果とは?
それでは波動関数と粒子の存在確率が復習できたところで、トンネル効果の説明に移りましょう。まずはイメージ的な説明を行います。
トンネル効果のイメージ
トンネル効果とは上で述べたように、波動関数がポテンシャル障壁を乗り越えて伝播する現象のことです。特に、本来伝播できない程の高さを持つポテンシャルを伝播してしまう現象と捉えれば良いでしょう。

なるほど。本来は物理的制約で突破できないはずのポテンシャルを粒子が突破してしまう現象ということですね。
これは粒子の波動性に由来する性質で、そもそも粒子の存在自体が空間的広がりを持っており、その存在確率が完全に\(0\)となる位置は存在しません。そのため、ポテンシャル障壁を貫通してしまう現象が起こりますし、そのポテンシャルが低いほどその効果は大きくなります。

身近な面白い現象としては「呼吸」や「光合成」などがあります。これらの化学反応は電子の伝達の際にトンネル効果を利用しているそうですよ。また、化学では分子の異性化やポテンシャルエネルギー曲線でこのような話が出てくることがあります。

古典力学と違って、ポテンシャル障壁が大きくても存在確率を考えないといけないわけですね。考えることが多くなりそうだ…
数式を用いたトンネル効果
この後は数式を用いてトンネル効果を示していきます。計算には特に興味がないという人はここまでを理解できれば良いでしょう。まずは1次元箱型ポテンシャルについて復習します。
1次元箱型ポテンシャルとトンネル効果
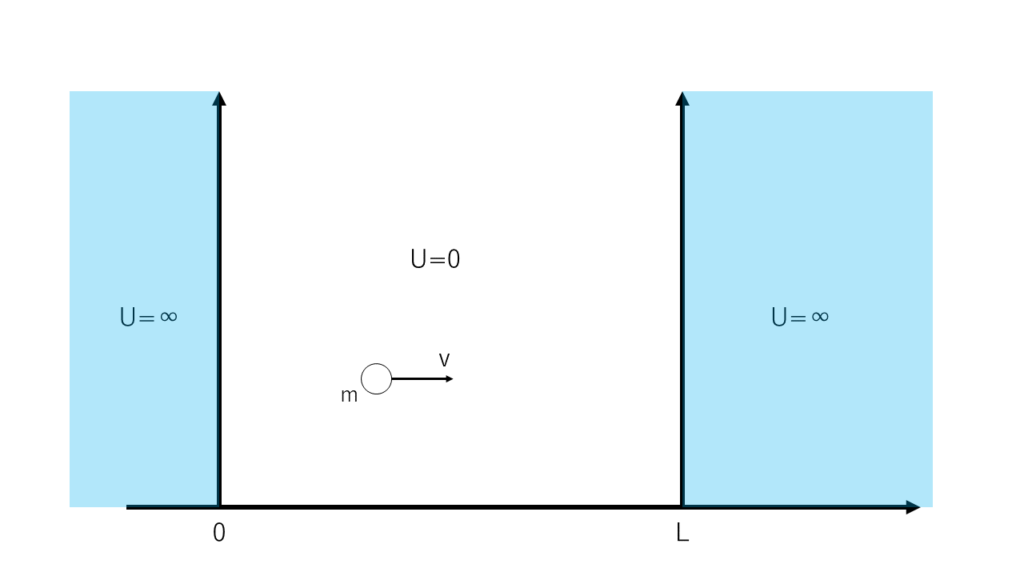
1次元箱型ポテンシャルでは\(0\leq x\leq L\)を満たす領域では、ポテンシャルが\(0\)ですが、それ以外の領域では無限大と考えましたよね。
この無限大のポテンシャルとして考えていた部分を、以下の図のように何かしら有限な値\(U_0\)として考えた状況のことを有限の箱型ポテンシャルといいます。
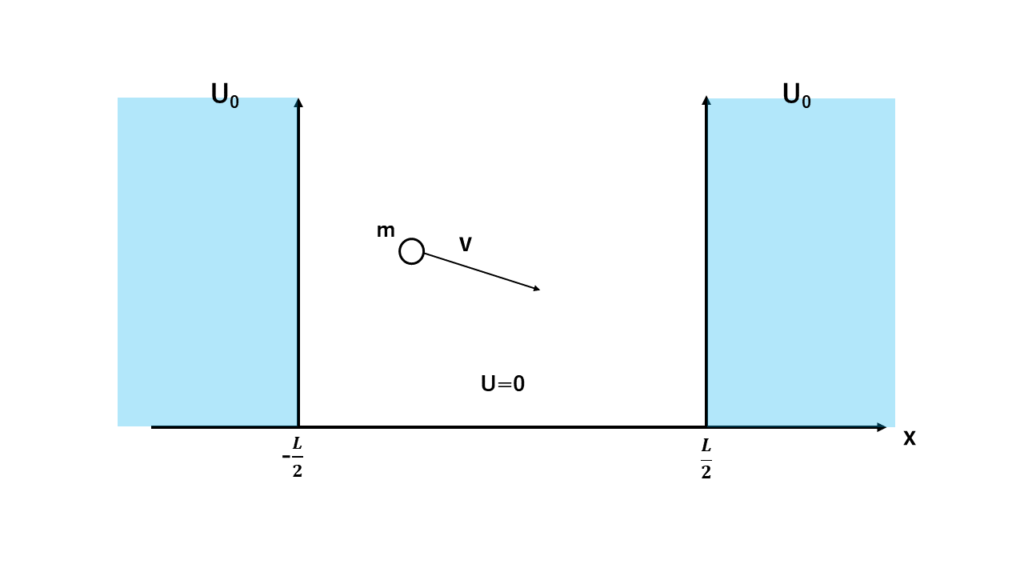
そしてこのような図であらわされる状況では、粒子のポテンシャルについて以下の式のような条件が成り立ちます。
$$U=0(-\frac{L}{2}\leq x\leq \frac{L}{2}のとき)$$
$$U=U_0(x\leq -\frac{L}{2}または\frac{L}{2}\leq xのとき)$$

なぜ座標の取り方が異なるのかはあとで説明しますが、こうすることで波動関数の式がうまくまとまります。ちなみに、ポテンシャルとは高校物理でいうところの位置エネルギーですよ、しっかり覚えていましたか?
シュレディンガー方程式の立式


それではいつも通りシュレディンガー方程式を立てていきましょう。もう見慣れてきたと思いますが復習からです。
シュレディンガー方程式の基本形は下のような形でした。
$$\hat{H}\psi=E\psi$$
これを基にして、今回考える有限の箱型ポテンシャルについてのシュレディンガー方程式を作っていきます。
置き換えによるハミルトニアン
今回の「有限の箱型ポテンシャル」はポテンシャルが無限大ではないことから、どこにでも粒子は存在可能なので2つの領域に分けて考えます。
箱の中に粒子があるとき
箱の中、つまりポテンシャルが\(0\)の部分に粒子があるときは、粒子のポテンシャルはもちろん\(0\)なので、粒子が持つ全エネルギーは運動量を用いることで下のように表すことができます。
$$E=\frac{p_x^2}{2m}+0=\frac{p_x^2}{2m}$$
この式中の運動量を演算子に置き換えることで得られるハミルトニアンは下の式のようになります。
$$\hat{H}=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}$$

1次元箱型ポテンシャルのときと全く同じだ!

そのとおりです。今回ポテンシャルが違うのは箱の外なので、箱の中に関しては1次元箱型ポテンシャルと全く同じになります。
箱の外に粒子があるとき
今回考えているポテンシャルは無限大ではないので、1次元箱型ポテンシャルとは異なり、箱の外であっても粒子は存在可能となります。
同じようにまずは粒子の全エネルギーから考えると、粒子のポテンシャルは\(U=U_0\)なので
$$E=\frac{p_x^2}{2m}+U_0$$
さらに運動量を演算子に置き換えるとハミルトニアンは
$$\hat{H}=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U_0$$
ほとんど先ほどと同じように見えますがポテンシャルが\(0\)ではなく\(U_0\)になっていることに注目です。
シュレディンガー方程式の全体像
それぞれのハミルトニアンが求まったので方程式の全体像を見てみましょう。
$$-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\psi=E\psi (-\frac{L}{2}\leq x\leq \frac{L}{2}のとき)$$
$$(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U_0)\psi=E\psi (x\leq -\frac{L}{2}または\frac{L}{2}\leq xのとき)$$
箱の中に粒子があるときと箱の外にあるときとで若干式が違いますね。これは今まで話してきた通り、ポテンシャルの違いによるものです。
シュレディンガー方程式を解く

1次元箱型ポテンシャルで学習したように波動関数は三角関数で表すことができます。1次元箱型ポテンシャルでは\(sin\)関数のみを用いましたがこれは境界条件として\(cos\)関数は不適だからです。

1次元箱型ポテンシャル中の箱の外では粒子の存在確率は\(0\)となります。つまり波動関数の値も\(0\)となります。これに接続するような関数は端点(\(x=0,L\))で\(0\)をとる\(sin\)関数が適当です。
しかし今回は原点の取り方を少し変えてあるので波動関数は
$$\psi(x)=A\sin{ax}+B\cos{ax}$$
として考えてみましょう。

原点の取り方は任意なので、今回の場合はこの式で導出しますがこの解き方が絶対というわけではありません。また1次元箱型ポテンシャルの式と同等のものなので、関数の見た目が違うだけで本質的には同じです。
さらに箱の外の粒子に対する波動関数は
$$\psi(x)=Ce^{-\beta x} (\frac{L}{2}\leq xのとき)$$
$$\psi(x)=De^{\beta x} (x\leq -\frac{L}{2}のとき)$$
とあらわされます。
波動関数の連続性
ここで波動関数の連続性について考えてみます。何も難しいことではなく、もしポテンシャルに不連続な点があっても急に粒子が持つ物理量(特に存在確率)は変化しないので関数は端点(\(x=0,L\))でも連続になっていなくてはいけません。
よって\(x=\frac{L}{2}\)において次の連立方程式が成り立ちます。
$$A\sin{(a\times \frac{L}{2})}+B\cos{(a\times \frac{L}{2})}=Ce^{(-\beta\times \frac{L}{2})}$$
また上式を微分すると下の式が得られます。
$$aA\cos{(a\times \frac{L}{2})}-aB\cos{(a\times \frac{L}{2})}=-\beta Ce^{(-\beta\times \frac{L}{2})}$$
さらに\(x=-\frac{L}{2}\)においても同様に考えると
$$-A\sin{(a\times \frac{L}{2})}+B\cos{(a\times \frac{L}{2})}=De^{(-\beta\times \frac{L}{2})}$$
$$aA\cos{(a\times \frac{L}{2})}+aB\cos{(a\times \frac{L}{2})}=\beta De^{(-\beta\times \frac{L}{2})}$$
の2式が得られます。

文字が多くて、困惑しそうですが頑張ってついてきてください。微分と連立方程式しかやっていないと思えば、少しは簡単に見えるかもしれませんね。
定数の決定
ここからはただの連立方程式です。文字がたくさんあって面倒くさいので、もしわかりにくいのであれば、全部まとめてほかの文字で置き換えたりすると楽に計算できると思います。
上で導出したそれぞれの式から定数\(C\)と\(D\)を消去すると
$$A[\beta\sin{(\frac{aL}{2})}+L\cos{(\frac{aL}{2})}]+B[\beta\cos{(\frac{aL}{2})}-L\sin{(\frac{aL}{2})}]=0$$
$$A[\beta\sin{(\frac{aL}{2})}+L\cos{(\frac{aL}{2})}]-B[\beta\cos{(\frac{aL}{2})}-L\sin{(\frac{aL}{2})}]=0$$
上記より$$A[\beta\sin{(\frac{aL}{2})}+L\cos{(\frac{aL}{2})}]$$
$$B[\beta\cos{(\frac{aL}{2})}-L\sin{(\frac{aL}{2})}]$$この2式はどちらも\(0\)とならなければなりません。
物理的に意味のある解になるためには
$$\beta\sin{(\frac{aL}{2})}+L\cos{(\frac{aL}{2})}=0かつB=0…①$$
$$\beta\cos{(\frac{aL}{2})}-L\sin{(\frac{aL}{2})}=0かつA=0…②$$
の2パターンを考えます。
有限な箱型ポテンシャルの波動関数
①のときは\(B=0\)なので\(\psi(x)=A\sin{ax}\)となりこれは奇関数ですね。

奇関数なので原点に関して対称となります。このため\(x=\frac{L}{2}\)と\(-\frac{L}{2}\)での値は符号が異なり、ここから\(C=-D\)を導くことができます。
②のときも全く同様に考えて\(\psi(x)=B\cos{ax}\)となり、偶関数なのでその性質を用いて\(C=D\)を導くことができます。
上記までの式をすべてまとめると有限の箱型ポテンシャルの波動関数を得ることができ、それぞれ下のような式になります。
奇関数のとき
$$\psi(x)=A\sin{ax}(-\frac{L}{2}\leq x \leq \frac{L}{2}のとき)$$
$$\psi(x)=Ce^{-\beta x}(\frac{L}{2}\leq xのとき)$$
$$\psi(x)=-Ce^{-\beta x}(x\leq -\frac{L}{2}のとき)$$
偶関数のとき
$$\psi(x)=B\sin{ax}(-\frac{L}{2}\leq x \leq \frac{L}{2}のとき)$$
$$\psi(x)=Ce^{-\beta x}(\frac{L}{2}\leq xのとき)$$
$$\psi(x)=Ce^{-\beta x}(x\leq -\frac{L}{2}のとき)$$
今回重要になるのは、1次元箱型ポテンシャルのときとは異なり\(x\leq -\frac{L}{2}または\frac{L}{2}\leq x\)のときでも、波動関数の値が\(0\)以外の値をとるということです。これが原因で最初に説明したトンネル効果が起こるのです。
今日の要点
「トンネル効果」とはミクロな世界において粒子が越えられないはずのポテンシャルの山を越えるという不思議な現象のことをいい、これは波動関数の値が箱の外でも\(0\)ではなくなることから導かれます。
日常的には実感することはありませんが、みなさんが使っているスマートフォンに使われる半導体といった電子の動きを高度に制御するようなものにおいてはこの効果は重要になってきます。
- 有限のポテンシャル中では粒子はポテンシャルの山をすり抜ける
- ポテンシャルの山をすり抜けることを「トンネル効果」という
- 数式上では波動関数の値が\(0\)でないことによって表現される

次回は極座標表現について解説します。これが使えるようになると分子や電子の回転運動を表す方程式についての理解が深くなりますよ。
付録
波動関数の形の違い
さて少し余談ですが波動関数に関して\(sin\)関数と\(cos\)関数、またはその組み合わせなどなぜ形が違うのか気になる人もいるかと思いますので少し解説します。
結論から言うとどのように表現しても物理的には同値です。これは高校で学習した「三角関数の合成」や「平行移動」を思い出してもらえば理解できるかと思います。\(sin\)関数と\(cos\)関数は位相がずれているだけなので平行移動すればぴったり重なりますね。そのためどちらを解に使っても位相のずれが出るだけで関数そのものが持つ意味に差はありません。
またその組み合わせ(線形結合)も三角関数の合成をしてしまえば\(sin\)関数に変換できるため結局は同じ意味を表しています。またこの場合は関数の取りうる最大値や最小値が変わってしまうので、波動関数で使う際は\(sin\)関数単体で用いる場合に比べて規格化定数が若干異なる場合があります。

そのためどのような形の三角関数を使っても意味は同じです。ちなみに線形結合とはそれぞれの関数を定数倍したものの和という意味です。この掛ける定数は実数に範囲なので負の数もOKとなります。
なぜ指数関数を使うのか?
これは波動関数の性質によるものです。
つまりあまりに原子核(今回の座標上では原点)から離れすぎたところに電子を見出す確率は限りなく\(0\)に近くなるため、\(x→∞\)、\(x→-∞\)で\(0\)に収束するような関数を使わなければなりません。そのため三角関数は使えなくなり、その代わりとして指数関数が使われます。他にも\(0\)に収束するような関数は山ほどありますが、オイラーの公式を用いて三角関数にも変換できる指数関数を用いるのが一般的になっています。
オイラーの公式
$$e^{ix}=\cos{x}+i\sin{x}$$
ちなみにこのトンネル効果は化学ではアンモニア分子の反転運動においてよく見ることになるでしょう。しかしこの現象を説明するには分光学等の知識も必要となってくるのでここでは割愛します。





コメント